Studiare il funzionamento di tutte le porte logiche di base per usare l’algebra booleana per descrivere e analizzare i circuiti digitali costituiti da combinazioni di porte logiche. Questi circuiti possono essere classificati come circuiti logici combinatoriali, perché, in qualsiasi istante di tempo t, il livello logico in uscita dipende dalla combinazione dei livelli logici presenti sugli ingressi solo in quell’istante di tempo t.
Un circuito combinatorio non ha caratteristiche di memoria, quindi la sua uscita dipende solo dal valore corrente dei suoi ingressi.
Qui, continueremo il nostro studio sui circuiti combinatori, la semplificazione dei circuiti logici. Verranno utilizzati due metodi: uno che utilizza teoremi di algebra booleana; l’altro che usa una tecnica di mappatura. Inoltre, verranno studiate semplici tecniche per la progettazione di circuiti logici combinatori per soddisfare un determinato insieme di requisiti. Uno studio completo sulla progettazione di circuiti logici non è uno dei nostri obiettivi, ma i metodi che introduciamo forniranno una buona introduzione alla progettazione logica.
La semplificazione dei circuiti digitali
Una volta ottenuta l’espressione per un circuito logico, potremmo essere in grado di ridurlo in una forma più semplice contenente meno termini o meno variabili in uno o più termini. La nuova espressione può quindi essere utilizzata per realizzare un circuito equivalente al circuito originale ma che contiene meno porte e connessioni. Per illustrare quanto detto, il circuito della figura (a) può essere semplificato per produrre il circuito della figura (b). Entrambi i circuiti eseguono la stessa logica, quindi dovrebbe essere ovvio che il circuito più semplice è più desiderabile perché contiene meno porte e sarà quindi più piccolo e più economico dell’originale. Inoltre, l’affidabilità del circuito migliorerà perché ci sono meno interconnessioni che possono essere potenziali guasti del circuito.
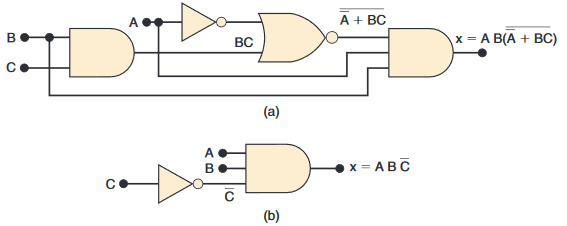
Un altro vantaggio strategico della semplificazione dei circuiti logici riguarda la velocità operativa dei circuiti. Ricordiamo dalle precedenti discussioni che le porte logiche sono soggette a ritardo di propagazione. Se i circuiti logici pratici sono configurati in modo tale che i cambiamenti logici negli ingressi debbano propagarsi attraverso molti strati di porte al fine di determinare l’uscita, non possono probabilmente funzionare tanto velocemente quanto i circuiti con meno strati di porte. Per esempio, dal confronto dei circuiti della figure (a) e (b) si nota che nella figura (a), il percorso più lungo che un segnale deve percorrere coinvolge tre porte, mentre nella figura (b), il percorso del segnale più lungo (C) coinvolge solo due porte.
La semplificazione algebrica
Si usano i teoremi di algebra booleana per semplificare l’espressione per un circuito digitale. Sfortunatamente, non è sempre ovvio quali teoremi dovrebbero essere applicati per produrre il risultato più semplice. Inoltre, non esiste un modo semplice per dire se l’espressione semplificata è nella sua forma più semplice o se sarebbe potuta essere ulteriormente semplificata. Pertanto, la semplificazione algebrica diventa spesso un processo di tentativi ed errori. Con l’esperienza, tuttavia, si può diventare abili nell’ottenere buoni risultati ragionevolmente abili. Gli esempi che seguono illustreranno molti dei modi in cui i teoremi booleani possono essere applicati nel tentativo di semplificare un’espressione.
Si vuol far notare che questi esempi contengono due passaggi essenziali:
- L’espressione originale è messa in forma SOP (Sum Of Product, cioè Somma Di Prodotti) da ripetute applicazioni dei teoremi di DeMorgan e moltiplicazione dei termini.
- Una volta che l’espressione originale è in formato SOP, i termini del prodotto vengono controllati per i fattori comuni e il factoring (la fattorizzazione) viene eseguito ove possibile. La fattorizzazione dovrebbe comportare l’eliminazione di uno o più termini.
Esempio 1.
Si consideri la figura seguente.
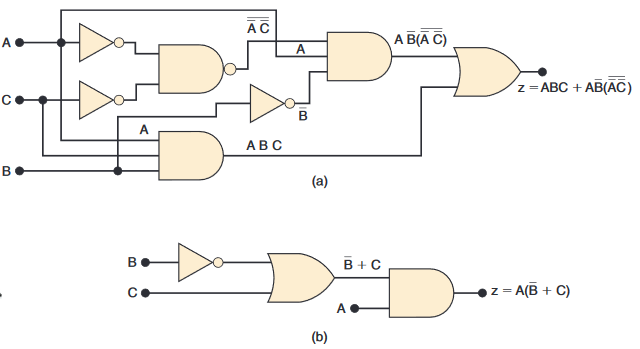
Soluzione.
Il primo passo è determinare l’espressione per l’output; il risultato è:
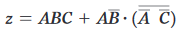
Una volta determinata l’espressione, di solito è una buona idea abbattere tutti i segni dell’inverter di grandi dimensioni usando i teoremi di DeMorgan e quindi moltiplicare tutti i termini.
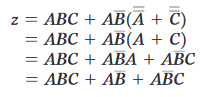
Con l’espressione ora in forma SOP, dovremmo cercare variabili comuni tra i vari termini con l’intenzione di factoring. Il primo e il terzo termine sopra hanno AC in comune, che possono essere presi in considerazione:
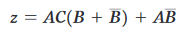
e, dal momento che qualsiasi variabile binaria messa in OR con la sua negata è sempre 1, si ottiene:
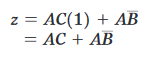
dai cui, raggruppando per A, alla fine:
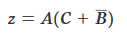
Esempio 2.
Si consideri la seguente espressione logica:
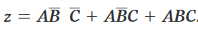
Consigliata anche la traduzione nello schema logico utilizzando le porte logiche elementari.
L’espressione è già in formato SOP.
Soluzione.
Legenda. Data una variabile booleana A, la sua negata -per problemi tipografici qui- si scriverà come A’.
Metodo 1.
I primi due termini dell’espressione hanno in comune il prodotto AB. Così:
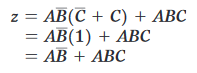
Possiamo fattorizzare la variabile A da entrambi i termini:
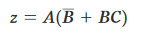
e allora, dalle leggi di Boole,:
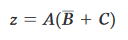
Metodo 2.
Dall’espressione originale, i primi due termini hanno AB’ in comune, e gli ultimi due termini hanno AC in comune. Come facciamo a sapere se calcolare AB dai primi due termini o AC dagli ultimi due termini? In realtà, possiamo fare entrambe le cose usando il termine AB’C due volte. In altre parole, possiamo riscrivere l’espressione come:
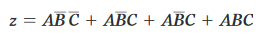
dove abbiamo aggiunto un termine aggiuntivo AB’C. Questo è valido e non cambierà il valore dell’espressione perché AB’C + AB’C = AB’C [secondo una identità dell’algebra di Boole].
Fattorizzando AB dai primi due termini e AC dagli ultimi due termini, si ottiene:
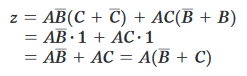
Esempio 3.
Semplicare la seguente espressione booleana:
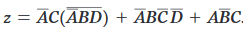
Soluzione.
Si applica De Morgan ul primo termine:
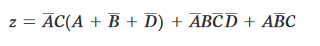
e per la proprietà distributiva:
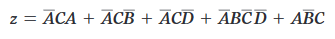
cioè:
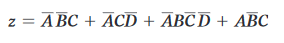
Si è ottenuta la desiderata forma SOP, nella quale bisogna cercare fattori comuni nei termini prodotto.
L’idea è quella di verificare il più grande fattore comune tra due o più termini di prodotto.
Per esempio, il primo e l’ultimo termine hanno il fattore comune B’C, mentre il secondo e il terzo termine condividono il fattore comune A’D’:
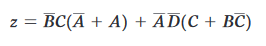
e alla fine:
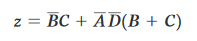
Altro metodo risolutivo.
Dalla forma SOP ottenuta:
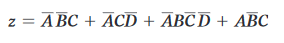
si sarebbe potuto fattorizzare C dal primo, secondo e quarto termine del prodotto fino a ottenere:
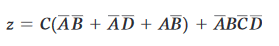
e ancora:
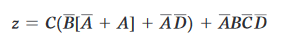
e ancora:
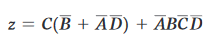
Moltiplicando si ottiene:
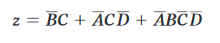
raccogliendo A’D’ dal secondo e dal terzo termine
dalla quale discende:
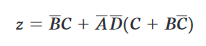
Esempio 4.
Semplificare la seguente espressione booleana.
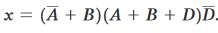
Soluzione.
Eseguendo la moltiplcazione si ottiene la forma SOP.
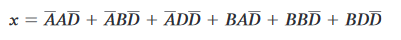
ottenendo:
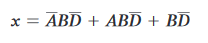
dalla quale si ha:
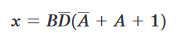
e infine
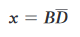
Esempio 5.
Semplificare il seguente circuito digitale.
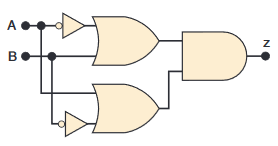
Soluzione.
Il circuto della figura ha la relazione ingresso-uscita:
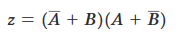
La forma SOP si ottiene moltiplicando:
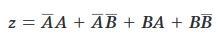
dalla quale, alla fine,
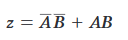
che tradotto in un circuito digitale si ottiene:
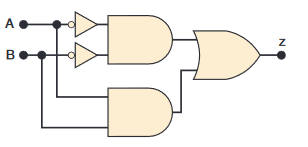
Se confrontato con il circuito originale, si nota che entrambi i circuiti contengono il medesimo numero di porte e collegamenti: in questo caso, il processo di semplificazione ha prodotto un circuito equivalente, ma non più semplice.
Semplificare:
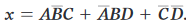
End Of Post




